The unkillable bird

Gaussian markets, power laws and the hyper cycle

I have been staring at Galton Boards this week and wanted to turn this into a post about the planning fallacy. But there’s just so much Stuff going on that I can’t help but abandon the planning fallacy and talk more generally about why our conception of the world is so muddled and why this is dangerous.

For a long time, I thought I understood Nicholas Nassim Taleb’s concept of a Black Swan. Like many others, I would parrot the description: “unpredictable, statistically possible, high impact”. But this week, as I was rewriting some content for my other stuff, I realised that I hadn’t understood it at all. And I’m not sure I’m alone in this. If we had truly absorbed this concept, we would change the way we respond to a lot of things - ranging from the planning of new projects to writing odes to Elon Musk’s specific brand of genius.

To try and explain how misguided we are, I am going to take you on a statistical journey written by a non-mathematician. If this sounds very dull, please stick with me. I think it offers a framing for a lot of the strange behaviour we are seeing in the US right now, even if it does not offer a remedy.

So let’s begin with the Galton Board. Francis Galton, a prolific Victorian eugenicist, discovered that:

Whenever a large sample of chaotic elements are taken in hand and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along

The beautiful form of regularity that he had discovered, is now known as the Bell Curve and it describes a normal distribution of data. This is pretty elementary statistics, but thanks to Nicholas Nassim Taleb’s impaction into our collective consciousness (itself a slow, slow, slow, slow, VERY FAST phenomenon) we now know that the Bell Curve is like every parent’s advice to their footloose teenage kid venturing afar for the first time: utterly insufficient in the face of the novel and precarious contexts in which they find themselves.

My breakthrough on all this, came when I learned about the Lévy flight foraging hypothesis. Suddenly, abstract descriptions of statistical phenomena came to life. And I am going to use this post to try and bring them to life for you.

Let’s begin, as I did, by imagining a Galton Board. A Galton Board is a structure arranged to allow marbles to fall between regularly placed pegs:

Source: Brener, Daniel. (2024). A hypothesis on ergodicity and the signal‐to‐noise paradox. Atmospheric Science Letters. 25. 10.1002/asl.1265.

If you pour marbles through a central funnel, they will trip gently through the pegs and assemble themselves into a neat, bell shaped configuration. This is most easily understood if you watch a simulation of the process (my thanks to Conundrumer’s Youtube channel for providing such a satisfying version below):

Dull right? Yes, until you understand what you are looking at. This is where the Lévy flight foraging hypothesis comes in. Instead of seeing marbles tripping through metal pegs, I invite you to visualise this simulation as birds foraging for food. Each marble represents a bird and each peg represents a decision choice. Because these marbles are independent of one another and regularly spaced, each bird has a 50/50 chance of either getting more food or less food depending on its decision choice as it hits the peg. Even if you know nothing about statistics, you may be able to see Galton’s ‘beautiful form of regularity’ building up in the simulation. If 1,000 birds go through the same experience, their eventual outcomes will not be equal. They will, instead, exhibit a magical symmetry where some birds get a bit more food and some birds get a bit less. Very few birds get extreme helpings (very small or very big).

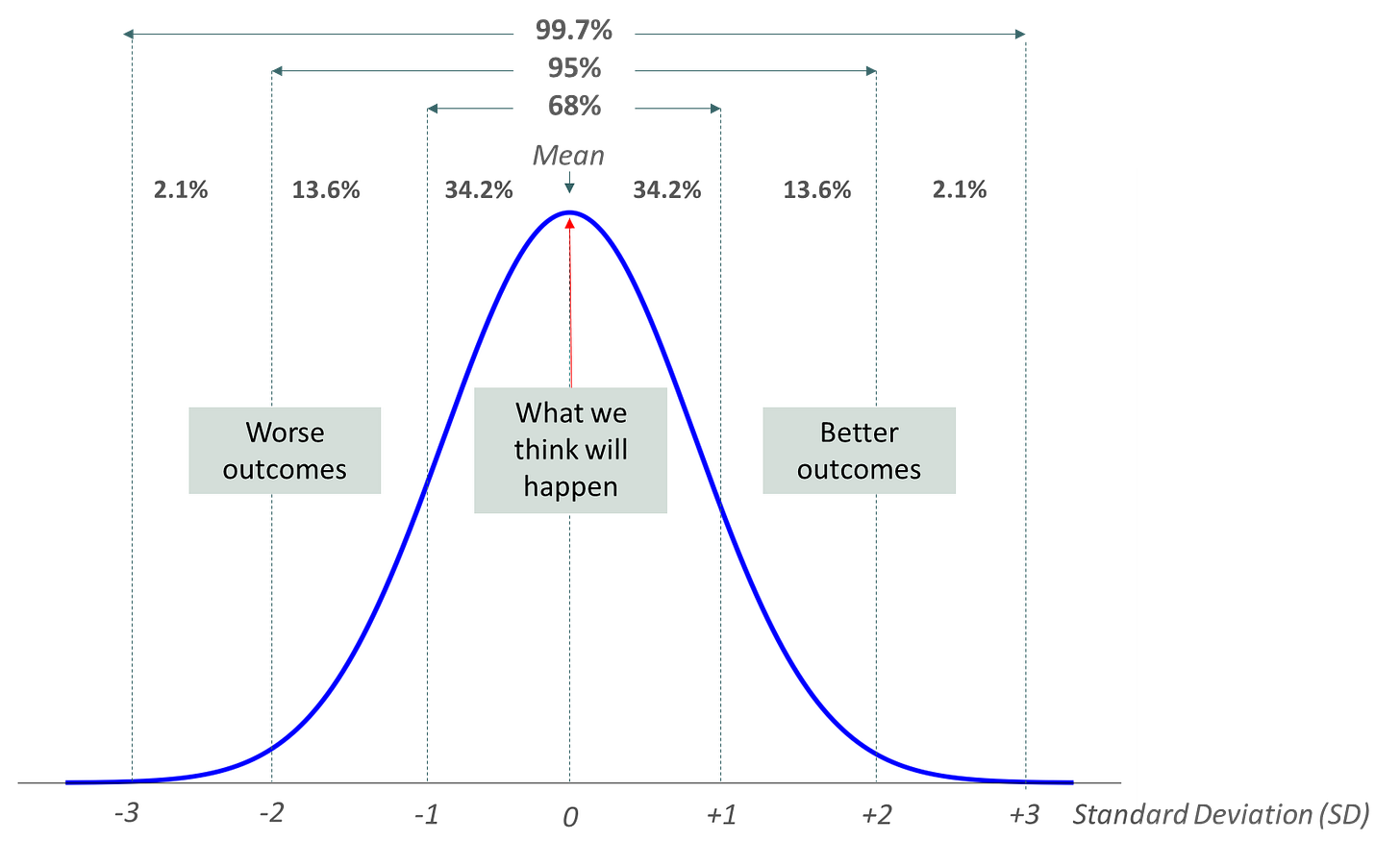
This type of distribution is called a Gaussian distribution where outcomes (where the marble lands) lie symmetrically either side of the mean (average). Thanks to Galton, we can even make statistical predictions about how many marbles will fall into each ‘bucket’ at the bottom of the Galton board:

Now Taleb’s contribution to all this was to help us see that our understanding of the world is fundamentally Gaussian. We tend to imagine nice symmetrical outcomes in systems that exhibit far from normal characteristics.

Some examples:

• it is a pretty common heuristic to assume that two people emerging from a similar environmental background are exposed to equal chances and capable of equivalent outcomes if they put in a bit of effort

• when we make plans, we tend to work out our average (anticipated cost / timing etc;) for the project and then add a little contingency to allow for slightly worse than average outcomes (a 10% buffer)

Or this, from an eminent behavioural psychologist (not identified), whose posts I enjoy enormously:

Ideally, people contributing to public discourse should be on platforms with a diverse range of political views. In this regard, Bluesky is limited in its ideological breadth.

That said, Twitter seems to be in continuous decline, with its algorithm making impartial and engaging discourse increasingly difficult to sustain.

It may be that the era of a general virtual town hall is over (bold italics mine).

I have no doubt that this individual would be able to give the pat explanation of a Black Swan event that I used earlier. But the characterisation of social media platforms as ‘Town Halls’ with a ‘diverse range of political views’, betrays the same simplistic Gaussian thinking. Social media platforms haven’t been regularly spaced peg boards since Facebook introduced the ‘Like’ button in 2007. In fact, social media platforms, like our global, political and economic systems, exhibit power law distributions not Gaussian distributions of outcomes.

And here I must make a confession - I led you astray about those birds facing 50/50 choices as they moved through the peg board. This isn’t the whole story. In fact, the Lévy flight foraging hypothesis discovered that animal foraging patterns exhibit a power law distribution. This means they conduct lots of small local searches for food but occasionally, they explore further afield. This is often described as the difference between exploitation and exploration. Or in layman’s language - as ‘tweaks’ and ‘leaps’. The important thing to understand here is that the tension between exploitation and exploration (tweaks and leaps) is fundamentally adaptive. If the bird only forages in its local area it will exhaust resources. If the bird only conducts long searches, then its offspring will go hungry if the bird falls from the sky. There is a risk reward calculation implicit in all this such that the bird makes lots of small, predictable searches accompanied by occasional, riskier leaps.

I have spent the past week trying to construct a Galton Board in my head to illustrate a power law. But there is no simple, regular way to conceptualise it.

So let me show you a diagram and try and explain it:

Source: User:Husky, Public domain, via Wikimedia Commons

In this example of a power law, instead of data distributing itself into a neat, symmetrical bell curve shape, we see an 80:20 power law. Applying this to our bird’s foraging behaviour, the long yellow tail approximates to the 80% of searches that are short and local. Meanwhile the green ‘fat’ tail (as Taleb describes them) approximates to the 20% of longer, exploratory searches. Unlike the Bell curve, the average of this distribution does not fall symmetrically in the middle. It will fall somewhere within that long yellow line (the ‘long’ tail as opposed to the ‘fat’ tail).

You may remember from the Gaussian diagram above, that 95% of all outcomes will fall within 2 standard deviations of the mean (average). I promised to avoid maths as much as possible in this post so I’m not going to explain standard deviations except to say that they describe how much each datapoint varies from the mean. In normal distributions, 95% of all datapoints will fall within 2 standard deviations (levels of variation) of the mean (average). This is useful for financial modellers because it means that if they know the average of their data sample, and have a reasonable number of datapoints, they can extrapolate the total range of possible outcomes for whatever they are modelling (by making their data look like a Bell Curve).

Unless …

The system they are modelling is not Gaussian!

Let’s imagine you run a company selling a broad mix of goods. Your average sale price is £10 and you decide to raise your prices by 5% taking the view that most people will be able to absorb a 50p increase (5% of £10). Unfortunately, your sales follow a power law distribution. Although your average sale is £10, most of your goods sell for a few pounds and a couple sell for £1,000. When you raise prices, you lose the customers who buy your expensive products and your business is crippled.

In a Gaussian system, an average and some datapoints allows you to conceptualise the entire system. In a power law distribution, knowing the average and a few datapoints tells you nothing.

So now it’s time to update my understanding of a Black Swan. Taleb wasn’t saying: “look out for outliers!”. He was saying that in a Gaussian system, outliers occupy a tiny percentage of the distribution of all possible outcomes. If you look at my chart above, you’ll see that 95% of all outcomes in a Gaussian distribution lie within 2 standard deviations of the mean (remember a SD represents how much each datapoint varies from the mean). But in power law distributions, extreme events can occupy far more than 5% of all outcomes. Not only this, they are likely to vary considerably from the mean.

The problem with all this is that when we imagine consequences to our decisions, we think of Gaussian outcomes: “extreme events are highly unlikely and we can cover them with a bit of contingency” when we should be thinking about power law outcomes: “very extreme events are likely and if they occur, the required buffer will keep multiplying until we can shut the system down”.

So what got me thinking all week was when does a Gaussian system turn into a power law? What are the conditions that drive this and what is a more appropriate way to think about outcomes in such systems?

Let me return to my foraging bird metaphor to try and explain this:

• Imagine birds foraging in their local environment - each bird will be subject to the same physical and resource constraints. i.e. no single bird will be able to carry especially more food or fly especially further than any other bird

• All things being (therefore) equal, the food outcomes distributed across the flock of birds, will follow a normal distribution. This is because each bird is flying through a theoretically regular environment with theoretically 50/50 decision choices at each peg and theoretically equal physical characteristics

• Now of course, in a real life environment, pathways will not be regularly spaced. Some birds may acquire useful adaptations (slightly longer feathers or slightly bigger beaks to carry more food). Some pathways will become more foraged than others

• We can describe these as local optimisations (adaptations). Local optimisations may lead to skews in the data (instead of symmetrically distributed outcomes, some pathways will yield significantly more food than others)

• But in a bounded system, these optimisations (better pathways, upgraded birds) will be subject to diminishing returns to scale. Diminishing returns are a beautiful way to stop one part of a system from racing away from other parts in the same system

• Because of diminishing returns, complex adaptive systems must continuously re-organise themselves to survive in their bounded environment

• This means local optimisations will be competed away, gradually. If one bird captures more resources at the expense of others, the overall population size will dwindle, offering fewer breeding opportunities

• If one pathway becomes depleted, there will be less food available and the population must either adapt (explore new pathways) or decline until resources have been restored

• These adaptations provide the stabilising feedback loops that constrain over-exploitation of resources by any part of a system

• They occur slowly, unconsciously and in a linear (1+1+1) fashion

Let me spell this out: in systems that are bounded (by time, physics, energy etc;) outcomes will tend towards stable, Gaussian patterns. Small, local adaptations will, with enough time and experimentation, be diffused or competed away. This is why human heights follow a Gaussian distribution. When everyone has broadly the same genetic make-up, grows up in a similar environment and is subject to the same physical / energy constraints, there will be no runaway outcomes in height. Adaptations (more protein, better healthcare) will be gradually diffused among the group over time allowing others to ‘catch up’.

Similarly, when students are exposed to the same curriculum and the same exam papers, their scores will distribute themselves in a Gaussian pattern. Data skews between schools can (should) be addressed with diffusion of best practice and resources to allow others to catch up.

All things being equal, we would expect bounded systems to exhibit a pattern of Gaussian behaviour followed by skews, followed by reversion to Gaussian behaviour.

So why do power laws exist?

• In Gaussian environments we see trial and error gradualism - at the first peg, maybe the bird gains +1 food. Then at the next peg it loses -1. Each additional unit of food can be added to the prior unit in a quantitative, linear manner (1+1)

• Through continuous optimisations (“tweaks”) the bird population may be able to sustain itself in a stable equilibrium within its environment

• In this Goldilocks zone, no change is too big or too small for the population to absorb

• But, stable equilibria can be disturbed by sudden change (climate change, competition from other animals, viruses etc;)

• Resources may become more scarce (or new environments may open up)

• In response to this, the birds will make occasional ‘leaps’, searching further afield for food

The bird foraging patterns now exhibit a power law distribution. Many local searches are punctuated by occasional, higher risk, long searches. The long searches are more likely to fail (than local searches) but when they succeed, they bring more food. Two things constrain these ‘leaps’:

• The physical structure of the bird - it cannot ‘leap’ too far without falling out of the sky, exhausted

• Failure - too many ‘leaps’ at the expense of local searches, will lead to more failure. The bird’s offspring will perish and the species will collapse

When the bird’s search pattern switches from a Gaussian to a power law environment, an unusual and critically important shift occurs:

Instead of short, local searches which yield linear outcomes (a bit more food, a bit less food), power laws describe conditions where long searches yield multiplicative outcomes (vast new food sources, or death of the bird). While local environments are subject to diminishing returns (the more you consume in the area, the more resources become depleted), global environments offer potentially unbounded (BUT RISKIER) returns.

If you take anything away from this post, let it be this:

• Local (searches) = small, bounded, incremental, low risk, predictable (Bell Curve) outcomes

• Global (searches) = huge, unbounded, exponential, high risk, unpredictable (Power Law) outcomes

Now, as I stated earlier in the post, this tension between small local searches (tweaks) and long, riskier searches (leaps) is fundamentally adaptive. It helps a system explore new opportunities as existing niches become depleted.

Imagine this as a business - the business establishes a successful product and gradually explores the (phase) space (the pegboard) of its local market through its sales and marketing activities. As it hits each peg (customers) it either makes a sale or doesn’t. In a competitive market where lots of other businesses are exploring the same (phase) space, incremental improvements make each peg (customer) a little more or less likely to convert to the business’s product. This is recursive so businesses constantly traverse the space making small adaptations to improve their chances at each peg.

But the market ‘space’ is finite - there are only so many customers for this product - so eventually, the product hits diminishing returns.

To stabilise itself within this market, the company must make some tweaks:

• it optimises itself in its local environment to give itself a slightly better chance of gaining a customer at each peg

And, it looks for new, more abundant environments by making some leaps:

• it explores new ‘distant’ markets

• it builds new, different products

The important thing about these tweaks and leaps is that they are in tension with one another. Too many leaps and the business’s capital is wasted on expensive failures. Too many tweaks and the business boxes itself into a fragile corner where one more optimisation will break the whole system (ahem, Boeing).

This beautiful emergent characteristic of biological systems leads to long periods of slow, trial and error incrementalism, as a species explores every part (peg) of its niche AND occasional leaps (new features, big adaptations - sometimes even speciation;).

Now anyone with an open mind and a casual interest in Economics has likely already stumbled upon a big open sore in the profession relating to this. One group of economists - often Nobel laureates - model economies as Gaussian systems in which the entire phase space of the economy under observation is considered to be explored by independent, individual units (birds making local searches or businesses selling products in a competitive market) leading to equilibrium states. Other economists (often described as heterodox economists) frame economies as adaptive systems (e.g.

Steve Keen

) or power conflicts between classes (e.g.

Yanis Varoufakis

) or power dynamics between market participants (e.g. Jonathan Nitzan).

The apotheosis of the equilibrium school of thinking is Friedrich Hayek, here writing in his extremely influential paper: “The Use of Knowledge in Society", 1945:

The peculiar character of a rational economic order is determined precisely by the fact that the knowledge of the circumstances of which we must make use never exists in concentrated or integrated form but solely as dispersed bits of incomplete and frequently contradictory knowledge … ‘planning’ in the specific sense in which the term is used in contemporary controversy means ‘central planning’ - direction of the whole economic system according to one unified plan. Competition, on the other hand, means decentralised planning by many separate persons. (bold italics, mine)

Hayek is imagining markets as businesses (birds) collectively traversing independent, regularly spaced pegs (customers), approximating to a self-stabilising ecological system, where prices deliver real time information about system state. But Hayek was writing in 1945, at a time of system collapse. Wholes had dis-integrated into parts. It was time to rebuild, and Hayek opposed John Maynard Keynes’ belief in top down Government money creation, to re-order the system. For Hayek, the system would be more resilient if it mimicked the behaviour of natural systems and self-organised itself into a state of equilibrium. For Keynes, this wasn’t a time for slow, trial and error exploration. Governments needed to jump and (literally) provide food, without all the slow, careful local searches.

Reader, we are living with the flaws that exist in both these paradigms.

Imagine a small market stall in medieval Europe. This market is frequented by many local customers who enter the market from different directions. In the course of a year, every part of the system is visited. Small advantages (optimisations) are found, exploited, then competed away.

This market is bounded in many ways. Physically, it occupies a small market square and cannot easily expand beyond these limits. The customers in the market are mostly limited to local inhabitants and some passing travellers who arrive slowly, through narrow streets, by horse or on foot. The workers in the market are similarly drawn from the local population and inhabit their own Gaussian market of (broadly) equal employment choices (agriculture, trades, domestic work etc;).

Of course, some optimisations will be successful enough to change the nature of the market - perhaps the bread stall will experiment with pies and develop a successful niche. But the market will always be fundamentally bounded by the number of customers and the size of the market square. The bread stall may expand a little but the number of customers willing to switch from bread to pies will be subject to diminishing returns. The amount of labour available to prepare pies will be limited to the local population. Soon other pie makers will enter the market with their own offerings and chip away at the bread stall’s advantage.

The medieval market satisfies Hayek’s view of a self-organising system where adaptations are competed away and prices find a level that reflects the bargaining power of free agents operating within an open market.

But now imagine, one day a passing merchant visits the market and has an idea. He proposes buying all the stalls on one side of the market and combining them. Then, he uses his influence to persuade the market manager to close off all but one entrance to the market. From now on, customers are funnelled through a narrow gap past stalls that appear separate, but which in fact have been combined into a bigger whole. As the ‘mega-stall’ offers all the goods available in other parts of the market, customers rarely traverse the entire market. Because of this, the incomes from the market participants are now skewed. Instead of a neat Gaussian distribution where no stall becomes much larger than any other, 80% of the market wealth is now concentrated in the hands of one owner. Gradually, the other stalls collapse or sell themselves out to the bigger stall. We all know what happens next - the combined stall uses its market power to charge customers more and pay suppliers and workers, less. Even when new owners set up stalls in the market, they quickly fail, or sell themselves off to the larger stall.

In this example, a Gaussian, linear market has transformed into a power law, exponential market. Feedback loops still exist but they can be described as “success to the successful” amplifying loops because most of the resources in the system have been captured by a single entity. Instead of resources being redistributed through competition and equal interactions between independent market participants (workers bargaining for higher wages, customers bargaining for lower prices, suppliers bargaining for fairer deals), all the power resides in one place. The mega-stall has become a new species.

Now the new ‘species’ uses its greater ‘energy’ to leap to a new niche. Just as a new, larger species of bird can forage across a greater area, the mega-stall now competes across regional markets, not within its own, local market. If all these other markets have undergone the same re-organisation, then the bird will once again be competing in a Gaussian market but often, the new species finds a lot of unconsolidated local markets. It then swoops in and grabs all the resources before these birds have had a chance to consolidate and re-organise. Now the bird is big enough to fly across a global region.

I hope it is becoming obvious that what economists call ‘free markets’ are far from free. In fact, they are markets in which a few small, initial changes in design have wreaked multiplicative effects on local markets, creating unbounded “success to the successful” feedback loops at a global scale.

Let me highlight a few features of all this:

• In power law markets, funnelling, merging and synchronisation of parts can produce exponential (multiplicative) outcomes

• These outcomes lead to qualitative changes (new species / types / environments), not quantitative system changes (a few more stalls, a few more sales, a few fewer customers)

• Once a new ‘species’ has formed, the cycle continues at different scales. Indeed the cycle may become scale invariant (i.e. endlessly repeating itself until it hits a physical boundary)

In our quaint view of markets, all participants (owners, consumers, workers) have equal-ish influence traversing regular-ish peg boards with 50/50ish outcomes. We imagine markets to be bounded and subject to diminishing returns such that small adaptations will eventually be diffused, copied and competed away. But power law systems operate differently.

Think back to the original Galton Board I described at the beginning of this post. Instead of independent, regularly spaced pegs, in a power law distribution, the pegs can synchronise, merge or create a funnel. This has an exponential effect opening up pathways that may encompass 10 or 100 or 1,000 pegs at once. If you can imagine this as foraging outcomes - instead of finding +1 or -1 food from each search, a bird may happen upon +1,000 units of food (or death!). In a market context, some participants will be put into a funnel and shipped to the far reaches of the distribution without any trial and error learning or slow, adaptive development. The development of the AI market is a good example of this. Instead of 1,000 companies slowly building up resilient new features through careful trial and error exploration, a few players made very ‘long leaps’ (raised huge amounts of capital from consolidated sources) and now control most of the market.

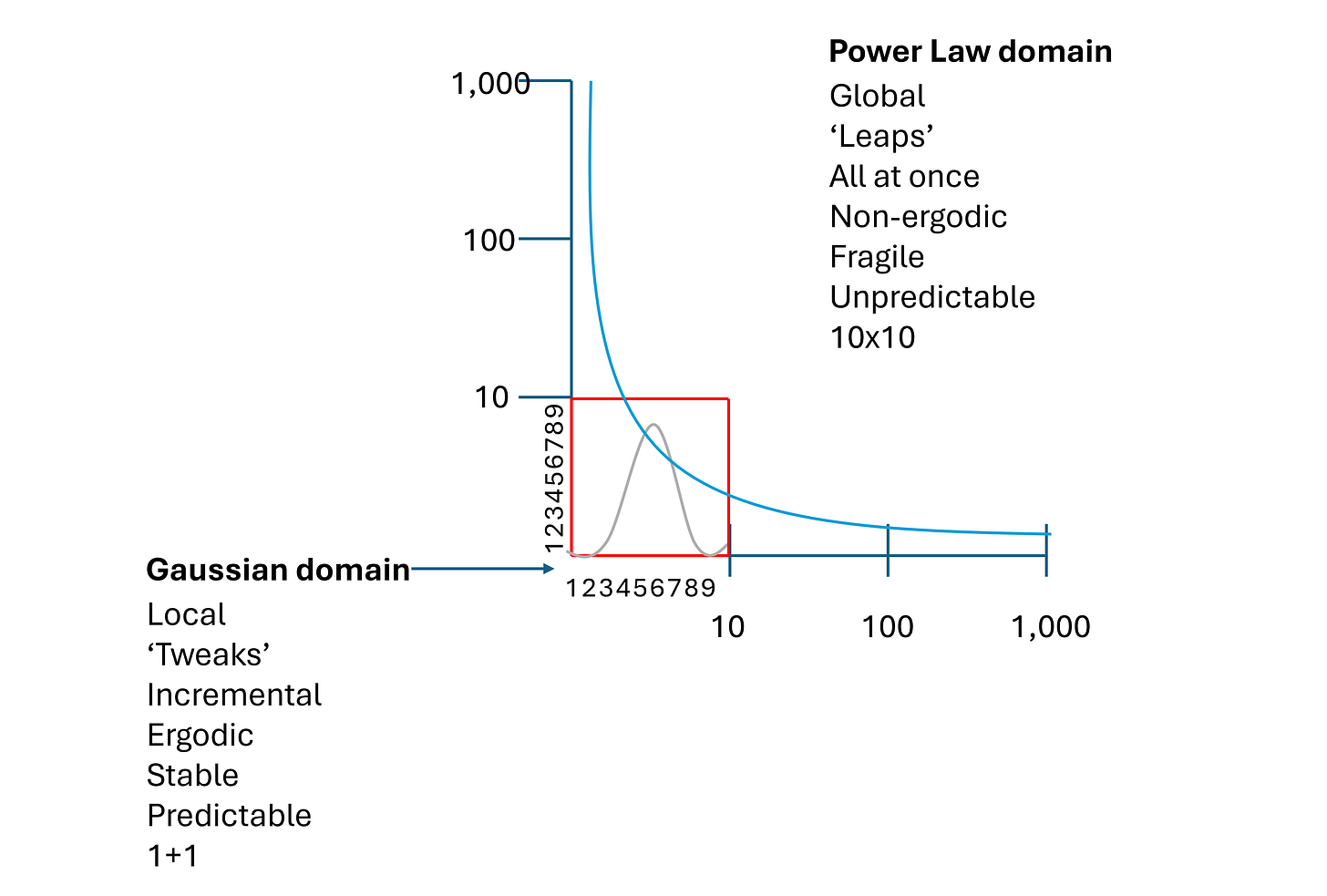
When we see illustrations of power law distributions in reports, the sheer craziness of their physics is obscured by the representative device of a logarithmic scale. A log scale allows the exponent (multiplicative) effect to be collapsed into a comprehendible size. I believe this contributes to the Gaussian fallacy of seeing Power Laws as inhabiting the same space as Gaussian distributions. They don’t. In the example below, I have tried to show that all the datapoints in a Gaussian can be squeezed into a linear (1,2,3,4,5) corner of a multiplicative power law scale. This still doesn’t do the job because I have used a log scale on the x and y axes (10, 100, 1,000). If I had represented this true to scale, the chart would extend well beyond the edges of your screen and into your surrounding environment. The Gaussian is tiny compared to the true size of an unbounded system operating according to a power law.

In our conception of how the world works we tend to imagine Gaussian environments where all actors start in the same place, all with the same 50/50 chances at each peg and where all parts of the system can be equally traversed. The more successful actors play their hands better and end up with more rewards.

But very few systems work this way. In reality, pegs are not neatly and evenly distributed with 50/50 outcomes. Some pegs are closer together, restricting pathways. Others are very broad - funnelling outcomes into a bucket. Some pegs close pathways off. The size of the board keeps multiplying with no physical boundaries.

In Gaussian systems a flock of birds (or population of customers in a market) can traverse an entire foraging space. This means that a single participant’s average outcome will converge to the ensemble average of all participants (known as ergodicity). This is true for local spaces but not so for global spaces. It would be impossible to explore every pathway in a global space and learn, through trial and error, the optimised pathway through the space. In non ergodic systems, the relationship between individual averages and the ensemble average breaks down as winners and losers emerge. This is an important characteristic of power laws which explains why they produce volatility and fragility, not resilience and stability.

Earlier, I scoffed at the description of social media as a ‘Town Hall’. If social media platforms offered users an ergodic interaction with their sites, this would be true (i.e. if all parts of the system could be traversed collectively, with equal attention, by the ensemble of participants).

But social media platforms create all the conditions for power laws:

• funnels (a single entry point into the system funnels your pathway through posts)

• network effects (Likes and retweets drive more interaction for some while other, more moderate viewpoints slip further into the long tail)

• Merge effects (Follows, memes such as “'#metoo”, combine similar viewpoints into concentrated blocks which amplify themselves)

• Interconnectedness (changes in one part of the system quickly propagate throughout the system)

• Sensitivity to initial conditions (a few posts by very few accounts can create enormous multiplicative effects that leap beyond the bounds of the platform into national politics)

• Tipping points (system criticality can be reached quickly and tip a Gaussian social interaction into a pile-on)

• Hyper cycles (leaps keep amplifying and collapsing, until the platforms become distorted around a few Black Swan accounts)

When we make predictions about Gaussian systems, we can assume a Bell Curve distribution of outcomes and build in a little slack to cover the 5% of very unusual but not hugely impactful outcomes. But if we are in a power law system, the system will be:

• unpredictable (we cannot assume neat symmetrical outcomes either side of the mean)

• multiplicative (buffers need to be at least 100% - possibly greater)

• (potentially) scale invariant (the impact of the Black Swan can keep amplifying beyond the original bounds and keep going until it hits a physical boundary)

• fragile (all the trial and error stability of the Gaussian system is lost in non-ergodic systems)

• very hard to reverse (cascades will keep amplifying until they hit a boundary, or collapse)

• synchronised - it will be impossible to pull small levers in one part of the system to stop a cascade. The only way to stop the cascade is to pull a lever that controls the entire system (e.g. “whatever it takes” bailouts)

Earlier, I mentioned that the original goal of this post was to talk about the planning fallacy. I intended to explain how it is easy to make good predictions about outcomes when our new projects are Gaussian. This is where we understand the landscape after long periods of trial and error / traversing the entire landscape. But if we leap into a new environment - planning something big, untested and unpredictable - then our best efforts at planning become useless:

• 10% (+0.1) contingencies need to switch to 100% (doubled) or 1000% (x10) contingencies

• Big projects (long flights) should be split into small, modular elements to reduce the risk of high impact failure

• Thresholds and tipping points should be ruthlessly scanned for, and Stop | Go gates introduced

• Physical boundaries should be introduced - resource / time boundaries to prevent ever longer flights

But in light of what is happening in the free world, the planning fallacy feels like the least of our problems. We undermined the ergodic, trial & error Gaussian economies that were possible after WW2 and replaced them with interconnected, synchronised, scale invariant hyper cycles. Instead of prioritising small, adaptive tweaks, our muddled thinking about “free markets” created the conditions for never-ending leaps:

• We curtailed the bargaining power of consumers, suppliers and workers

• We ripped out anti-trust laws and allowed companies to merge and speciate

• We prevented diffusion of adaptations by strengthening patent systems and forcing compliance through the courts

• We backstopped collapses allowing fragile systems to regroup, re-connect and and amplify further

• We removed physical boundaries to growth with money printing and debt creation

• We removed physical constraints to speculative money markets with deregulation

• By removing boundaries we removed the discipline of diminishing returns

• We allowed banks to create money and pump it into unconstrained asset inflation

• We allowed our over-consolidated, back-stopped, unconstrained system to leap into developing countries and gobble up their resources while saddling them with debt

• We allowed a few birds to become so big and so fat and so unbounded that when they hit planetary limits (diminishing returns), they started feeding off their own species

And this is where we find ourselves. There is a longer and longer tail of hungry birds and a tiny group of fat, unkillable birds. Instead of bounding our systems and discouraging long leaps by allowing riskier searches to fail, we built a safety net for them. Instead of slowing entrance to local markets and encouraging resilient, adaptive competition that benefitted all participants, and allowed participants to catch-up, we interconnected our markets, ripped out all the stabilising feedback loops and let rip with “success to the successful” loops.

We called all this: “free markets” and allowed these grotesque birds, fattened on fiat money, to leap from local to regional to global markets in a matter of decades. Without trial and error experimentation. Without slow, careful adaptation. And now, finally, they have hit a wall:

• declining fossil fuel resources

• declining demand (from indebted customers)

• unsupportable public debt levels

• competitive threats from beyond the system

So what do they do? They start eating their own species in a desperate scramble to make one more amplifying leap. The behaviour we see in the US is caused by a group of fat, unkillable birds who refuse to live within their means or compete on equal terms.

They recognise that our current system has hit a physical limit. They know that there is little scope for trial and error or adaptation in such a highly ordered, interconnected system. And they see that there is little more that can be squeezed from independent market participants (workers, customers, suppliers).

So they have given up on markets altogether and grabbed control of the state. They do not want a system of independent, individual customers collectively exploring a space filled with independent, individual companies. They do not want ergodic ‘Town Hall’ spaces where opinions can be explored collectively with no individual pathway promoted by biased algorithms. They want to consolidate their power and become a mega-species that feeds directly from the tank - the Federal Reserve. This species is unbounded by diplomatic etiquette or global rules. It has a military safety net strung underneath it allowing it to leap from sovereign state to sovereign state and forage for their resources before they have a chance to re-organise. Indeed, this hyper cycle is amplifying so quickly, it looks likely we’ll soon be left with just one fat, unkillable bird running everything.

So, is there any hope? Yes, of course! This is not our first rodeo. We have seen forces that believe they can re-order the world from the top down before. Their consolidation of power is the very source of their weakness. There is still much variation and adaptability in our system. The parts can re-organise, recombine and rebuild resilience. It will be painful and difficult, but bottom-up adaptation creates true strength. While they build their house of cards ever higher, we will release collective energy and build something stronger. I refuse to give up hope but we must confront the false narratives of efficiency, free markets and free speech with truth. Markets and speech can never be free in worlds where a few unkillable birds control everything.